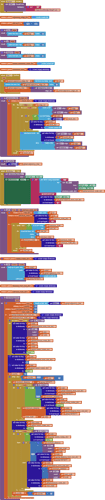
Dijkstra's Shortest Path Algorithm in blocks

App Showcase
1

This is an implementation in blocks of Dijkstra's Shortest Path Algorithm, with a sample graph and test framework.

It is a tool to find the shortest or lowest cost path from one node to another node in a weighted graph.

This has applications in route planning, and might be useful for students wanting to build their own campus map apps.

References:
https://www.google.com/search?q=Dijkstra's+algorithm

This particular implementation is based on C code at

Sample run:
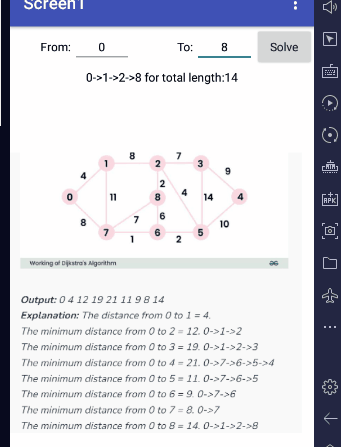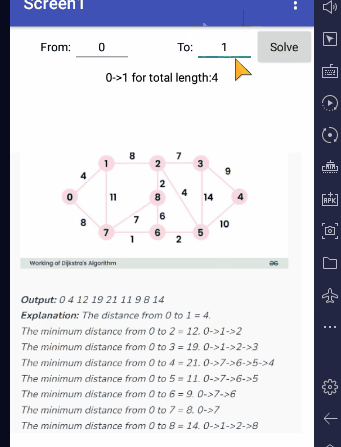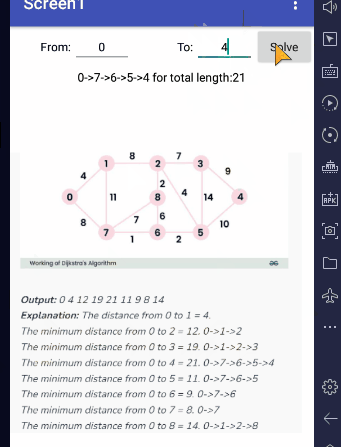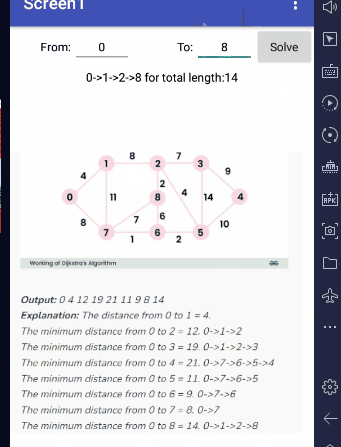
Sample run

Input graph, in sparse (one row per edge) form:

Sample CSV File 
Node1,Node2,Distance
0,1,4
0,7,8
1,0,4
1,7,11
1,2,8
7,0,8
7,1,11
7,8,7
7,6,1
2,1,8
2,8,2
2,5,4
2,3,7
8,2,2
8,6,6
8,7,7
6,7,1
6,8,6
6,5,2
3,2,7
3,4,9
3,5,14
4,3,9
4,5,10
5,6,2
5,2,4
5,3,14
5,4,10

Please note that the nodes don't have to be numbers (0-8).
They can be place names (columns 1 and 2) (PoeHall302, Boston, NYC, Paris, etc.) and the costs (column 3) can be your own measures in a common measure like time or distance or air fare.

Equivalent C code

Equivalent C code:

// Implementation of Dijkstra's Algorithm in C  
  
// importing the standard I/O header file  
#include <stdio.h>  
  
// defining some constants  
#define INF 9999  
#define MAX 10  
  
// prototyping of the function  
void DijkstraAlgorithm(int Graph[MAX][MAX], int size, int start);  
  
// defining the function for Dijkstra's Algorithm  
void DijkstraAlgorithm(int Graph[MAX][MAX], int size, int start) {  
  int cost[MAX][MAX], distance[MAX], previous[MAX];  
  int visited_nodes[MAX], counter, minimum_distance, next_node, i, j;  
  
  // creating cost matrix  
  for (i = 0; i < size; i++)  
    for (j = 0; j < size; j++)  
      if (Graph[i][j] == 0)  
        cost[i][j] = INF;  
      else  
        cost[i][j] = Graph[i][j];  
  
  for (i = 0; i < size; i++) {  
    distance[i] = cost[start][i];  
    previous[i] = start;  
    visited_nodes[i] = 0;  
  }  
  
  distance[start] = 0;  
  visited_nodes[start] = 1;  
  counter = 1;  
  
  while (counter < size - 1) {  
    minimum_distance = INF;  
  
    for (i = 0; i < size; i++)  
      if (distance[i] < minimum_distance && !visited_nodes[i]) {  
        minimum_distance = distance[i];  
        next_node = i;  
      }  
  
    visited_nodes[next_node] = 1;  
    for (i = 0; i < size; i++)  
      if (!visited_nodes[i])  
        if (minimum_distance + cost[next_node][i] < distance[i]) {  
          distance[i] = minimum_distance + cost[next_node][i];  
          previous[i] = next_node;  
        }  
    counter++;  
  }  
  
  // printing the distance  
  for (i = 0; i < size; i++)  
    if (i != start) {  
      printf("\nDistance from the Source Node to %d: %d", i, distance[i]);  
    }  
}  
  
// main function  
int main() {  
  // defining variables    
  int Graph[MAX][MAX], i, j, size, source;  
  // declaring the size of the matrix    
  size = 7;  
    
  // declaring the nodes of graph  
  Graph[0][0] = 0;  
  Graph[0][1] = 4;  
  Graph[0][2] = 0;  
  Graph[0][3] = 0;  
  Graph[0][4] = 0;  
  Graph[0][5] = 8;  
  Graph[0][6] = 0;  
  
  Graph[1][0] = 4;  
  Graph[1][1] = 0;  
  Graph[1][2] = 8;  
  Graph[1][3] = 0;  
  Graph[1][4] = 0;  
  Graph[1][5] = 11;  
  Graph[1][6] = 0;  
  
  Graph[2][0] = 0;  
  Graph[2][1] = 8;  
  Graph[2][2] = 0;  
  Graph[2][3] = 7;  
  Graph[2][4] = 0;  
  Graph[2][5] = 4;  
  Graph[2][6] = 0;  
  
  Graph[3][0] = 0;  
  Graph[3][1] = 0;  
  Graph[3][2] = 7;  
  Graph[3][3] = 0;  
  Graph[3][4] = 9;  
  Graph[3][5] = 14;  
  Graph[3][6] = 0;  
  
  Graph[4][0] = 0;  
  Graph[4][1] = 0;  
  Graph[4][2] = 0;  
  Graph[4][3] = 9;  
  Graph[4][4] = 0;  
  Graph[4][5] = 10;  
  Graph[4][6] = 2;  
  
  Graph[5][0] = 0;  
  Graph[5][1] = 0;  
  Graph[5][2] = 4;  
  Graph[5][3] = 14;  
  Graph[5][4] = 10;  
  Graph[5][5] = 0;  
  Graph[5][6] = 2;  
  
  Graph[6][0] = 0;  
  Graph[6][1] = 0;  
  Graph[6][2] = 0;  
  Graph[6][3] = 0;  
  Graph[6][4] = 2;  
  Graph[6][5] = 0;  
  Graph[6][6] = 1;  
  
  source = 0;  
  // calling the DijkstraAlgorithm() function by passing the Graph, the number of nodes and the source node  
  DijkstraAlgorithm(Graph, size, source);  
  
  return 0;  
}

Source:
Dijkstras_algorithm.aia (213.5 KB)

Blocks:

blocks
blocks947×4505 576 KB

6 Likes
2

Incorporating this code in your app, and ideas for expansion:

The distance matrix for this app sample was developed by typing in the nodes and costs into a Google Sheet, to take advantage of the tab and Enter keyboard actions that sped up the manual data entry from a picture of the sample graph.

If you have floor plans in .png format, you can use them as Canvas background images to capture room coordinates (x,y) and names of nodes for your graph.
Code an input screen to collect Canvas touch points for each node on each background image, and to enter names for them.
Then add input dialogs to enter costs between chosen node pairs on that particular subgraph.
You can then ties the subgraphs together with off-map edges.

3 Likes
3

can you show me the design that you use
please??

4

The app's Designer screen?

Download the aia file at

and import it.